

Applet: Katie Dektar
Text: Marc Levoy
Technical assistance: Andrew Adams
In the preceding applet, we discussed the range of colors (called the gamut) produced by mixing primary colors additively - as in television sets and computer displays, versus mixing them subtractively - as in printing. But what is meant by additive versus subtractive mixing? How does each work at the level of individual wavelengths? And what are the "right" primaries anyway - red, green, and blue? Or cyan, magenta, and yellow? Or red, blue, and yellow, as we learned in nursery school?
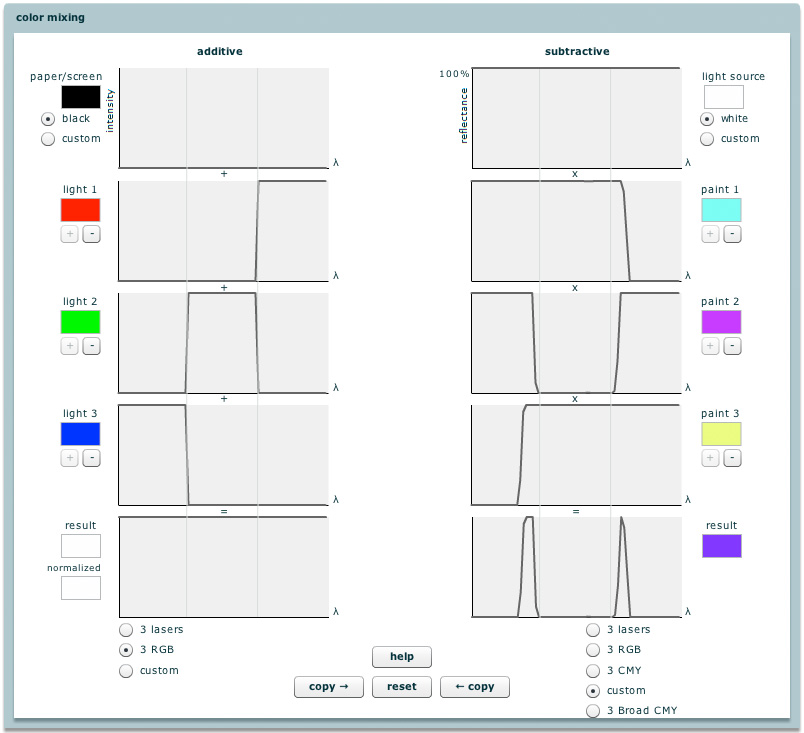
In our first version of the applet (above), we begin with three lasers, labeled "light 1" through "light 3". Beside each light is a spectral power distribution (SPD). Although wavelengths aren't labeled in this applet, short wavelengths (blues) are on the left side and long wavelengths (reds) are on the right. The SPD of a laser is a narrow spike (nearly a single wavelength). If the lasers are aimed at a common spot on a black wall, then due to the superposition property of light, we obtain an SPD that is the sum of the three component SPDs. This means we add them together wavelength by wavelength. The resulting SPD is shown at the bottom. As you would expect, the sum of these three particular lights, each consisting of one spike, is an SPD having three spikes at the obvious wavelengths. To its left is a "result" color, as would be seen by a person of normal color vision. We compute this color from the SPD using a set of RGB matching functions as described in our introductory applet on the trichromatic theory of color vision. In this case the resulting color is white. (It looks a bit pink on my monitor, but never mind.)
Now click on the "3 RGB" button at the bottom of the "additive" column. You now see an abstracted but plausible set of red, green, and blue lights. They have broader spectra than the lasers, but each is concentrated in one part of the visible spectrum. Since the rising and falling edges of the three spectra are aligned, it should come as no surprise that the additive mixture of these lights is an equal-energy SPD, shown at the bottom. It should also come as no surprise that this SPD looks white. since white is what we normally associate with a light source having all wavelengths in equal quantities, like the sun. What's more strange is that we could produce white in two such completely different ways - using an equal-energy light and using three lasers. Issac Newton observed this fact - that he could match the appearance to his eye of sunlight using an additive mixture containing only a few wavelengths, but he couldn't explain it. Formally, we say that an additive mixture of these three wavelengths is a metamer for equal-energy white. A proper explanation of metamerism awaited the work of Young and Helmholtz, in the 19th century.
Before moving on, note that the colors shown beside the three lights in "3 RGB" mode look similar to those of the three lasers. We computed these colors from their SPDs using matching functions, as described earlier. Their similarity to the lasers is simply another example of metamerism! Want to play? Draw your own spectra, by clicking on the SPDs and dragging! If the color you make is very dark - almost black - then it will be displayed as you made it in the "result" box, and brighter in the "normalized" box.
Additive mixing was exemplified in this applet by shining multiple lights onto the same spot. Another example of additive mixing is textiles, in which differently colored threads appear in close proximity, and therefore their colors mix additively in our eye. On the other hand, if you reflect light from a colored surface, or if you place a colored filter in front of a light, then some of the wavelengths present in the light may be partially or fully absorbed by the colored surface or filter. If we characterize the light as an SPD, and we characterize absorption by the surface or filter using a spectrum of reflectivity or transmissivity, respectively, i.e. the percentage of light reflected or transmitted at each wavelength, then the SPD of the outgoing light can be computed by multiplying the two spectra. This multiplication is (misleadingly) called subtractive mixing.
To see how this works, look at the subtractive side of the applet above. With the "3 lasers" button pressed, "filter 1" through "filter 3" represent extremely narrowband filters, i.e. filters that permit light of only one wavelength to pass through. Filters this narrow are difficult to achieve in practice, but never mind. Multiplying the light's SPD, which is set to equal-energy white, by the three absorption spectra in sequence (think of three filters stacked one atop the other and placed in the path of the light) leaves a zero-everywhere SPD, which looks black. Now switch to "3 RGB". It produces black as well. These are the same filters we abstractly placed in front of white lights to produce the three colored lights of our additive system, but whereas the additive system produced white, the subtractive system produced black! The key is that in one case we were superimposing colored lights, so we added the spectra wavelength by wavelength, while in the second case we were stacking colored filters, so we multiplied the spectra wavelength by wavelength. The results of adding versus multiplying spectra are very different.
You're probably thinking to yourself that of course red, green, and blue filters don't work in a subtractive system; the three subtractive primaries are cyan, magenta, and yellow. Are you sure about this? Click on the "3 CMY" button on the applet above. Here are three filters that individually look about right. You can alternatively think of them as three printer inks. Their mixture certainly makes black. That's good; a printer needs a good solid black. Now stroke horizontally across the top of the 2nd (magenta) filter's spectrum, turning its transmissivity to 100% at all wavelengths. (Equivalently, click repeatedly on the minus button "-", until the magenta filter's spectrum's "dip" disappears.) This effectively deactivates this filter. What happens? You still get black! Shouldn't you get a mixture color - maybe green? Reset the applet, select "3 CMY" again, and try deactivating the first or third filter. All such combinations produce black. This evidently isn't a useful subtractive mixing system.

|

|

|

|
1 | 2 | 3 | 4 |
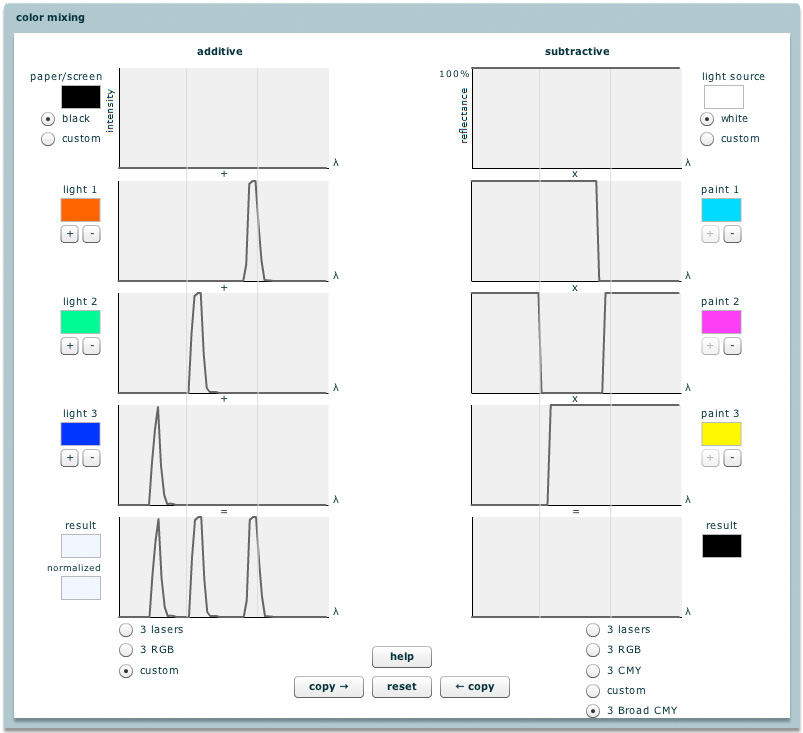
Let's try a few more things. First, try drawing your own subtractive filters. Note that your filters don't have to look exactly cyan, magenta, or yellow, in order to create a nice range of mixture colors. Look for example at the orange filter #3 I've created in example 1 above. But notice that if you create filters whose spectra overlap too much, then you can't make black, as shown in example 2. Second, try drawing your own additive filters. Note that they too don't have to look exactly red, green, or blue. Look at the nice orange light #1 I've created in example 3. But notice that if you create filters whose spectra overlap at all, then while you can still make white when they superimpose, the individual primaries are no longer saturated - they look pastel, as in example 4. As a result, you will be unable to make fully saturated colors in such a system.
So what have we learned? First, we've learned that primaries in an additive system don't need to be red, green, and blue. They just need to be well separated along the spectrum. Returning to the first color applet, the axes they define in rho-gamma-beta colorspace should enclose a large gamut volume. We've also learned that they should be narrow spikes, if we are to produce saturated colors. In rho-gamma-beta colorspace, narrow spikes correspond to primaries that touch the locus of spectra colors. Sure enough, such primaries enclose larger gamuts than more pastel primaries, which fall inside the spectral locus.
On the subtractive side, we've learned that the primaries don't need to be cyan, magenta, and yellow. They could even be red, yellow, and blue - the colors of nursery school paints! However, they need to be spectrally wide, if we are to achieve a full range of mixture colors. Unfortunately, we can't use rho-gamma-beta colorspace to visualize subtractive mixing, since spectra that are multiplied instead of added don't satisfy the fundamental property of linearity that is required to make this colorspace work.
Finally, although this applet doesn't provide the ability to mix more than three primaries, we already showed (in that earlier applet) that adding more primaries provides a wider range of colors.
© 2011 Marc Levoy